 |
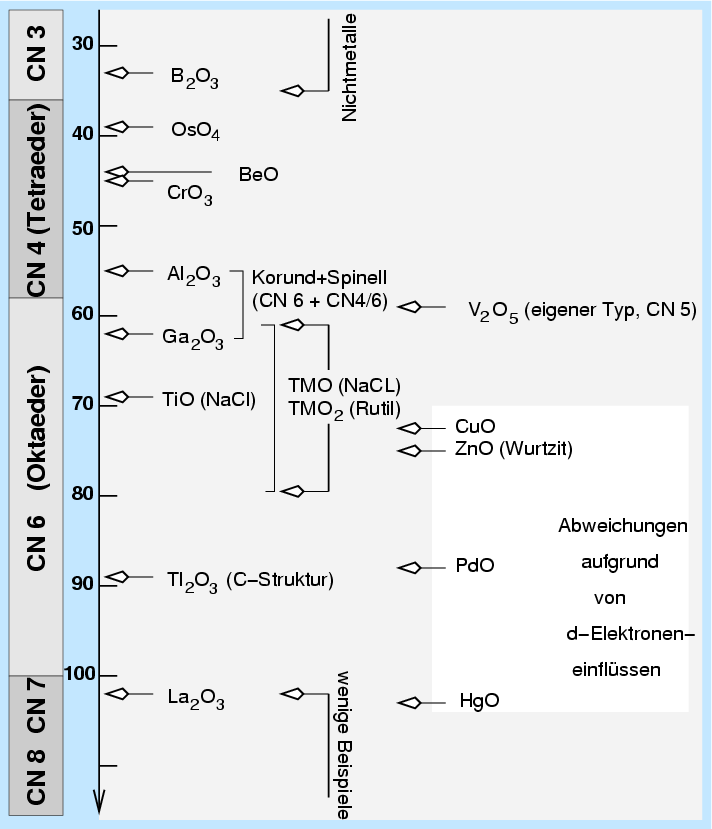
| Abb. 4.2.1. Radienverhätnisregel am Beispiel der Oxide ‣ SVG |
| cr_home | Metalle | Nichtmetalle | FK-Chemie | Methoden | Interm. Phasen | Oxide | Silicate | Strukturtypen |
| ⇦ | Inhalt | Einleitung | Kovalente FK | Metalle | Ionenkristalle | Literatur | ⇨ |
Die qualitative Folgerung für die Maximierung der Gitterenergie ist, dass die Kationen von möglichst vielen Anionen umgeben sein sollten (und umgekehrt) und Kationen und Anionen 'zueinander passen' sollen. In der Strukturchemie von Ionenkristallen gelten hierzu die empirischen Pauling-Regeln, die vereinfacht die Minimierung der potentiellen Energie wiedergeben:
| Um jedes Kation wird ein Koordinationspolyeder gebildet. Der Abstand zwischen Kation und Anion ist durch die Summe der Ionenradien bestimmt, die Koordinationszahl dagegen vom Radienverhältnis. |
Genauer:
Nach Einführung von Polyedern um die Kationen
(Festlegung der Koordinationszahl) und bei Zuordnung von Ionenradien zu den
einzelnen Teilchen, wird die Koordinationszahl (CN) vom Radienverhältnis,
die Atomabstände vom Wert der Ionenradien bestimmt.
Demnach bestimmt also das Radienverhältnis wesentlich die Koordinationszahl
und damit auch den möglichen Strukturtyp.
Konkret sind die Koordinationszahlen der Kationen
in Oxiden (rein geometrische Betrachtung, Ligandenfelder vernachlässigt, Radius von
O2- = 140 pm) in Tabelle 4.2.1. mit aufgeführt.
| CN=4 (Tetraeder) | CN=6 (Oktaeder) | CN=8 (Würfel) | |
| Radienverhältnis (untere Grenze) | 0.225 | 0.414 | 0.732 |
| Kationenradius in Oxiden [pm] | 36 | 58 | 102 |
| Zusammensetzung | Strukturtypen | ||
| A2B | anti-CaF2 | - | - |
| AB | ZnS (Zinkblende, Wurtzit) | NaCl | CsCl |
| AB2 | SiO2 | Rutil, CdCl2, CdI2 | CaF2 |
Beispiele:
Bekanntestes Beispiel ist die Strukturtypenfolge (ZnS, NaCl, CsCl)
(s. z.B. Chemie der Metalle in Kap. 2.3.)
bei einfachen Salzen.
Bei Silicaten ergibt sich aufgrund der Ionenradien von Si4+ und O2-
unmittelbar die Koordinationszahl 4 für Silicium gegen Sauerstoff.
Die Werte für andere Kationen entsprechen den in der Tabelle 4.2.1. angegebenen.
Sind in einer Verbindung unterschiedliche Kationen vorhanden, dann
können eventuell nicht alle ideale Verhältnisse finden. In diesem Fall
weichen die Kationen mit der geringsten Ladung und dem größten Radius auf andere
Koordinationszahlen aus. Beispielsweise liegt Natrium im Sodalith
Na8[Si6Al6O24]Cl2
nicht wie sonst mit der Koordinationszahl 6, sondern nur mit einer
Koordinationszahl von 4 vor, während Si (höhere Ladung!) in CN 4
verbleibt.
 |
| Abb. 4.2.1. Radienverhätnisregel am Beispiel der Oxide ‣ SVG |
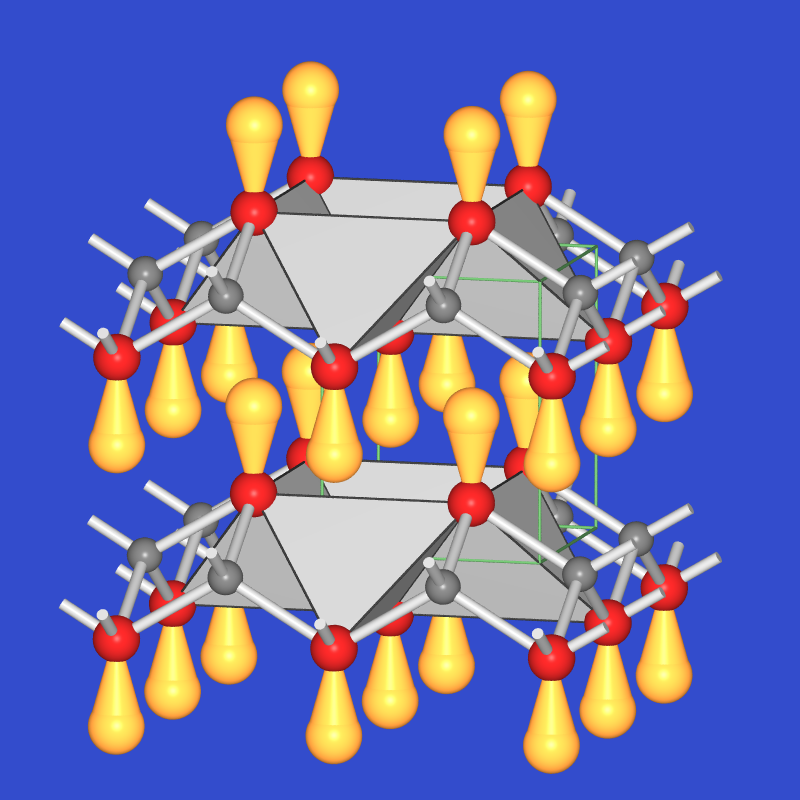
Bei Hauptgruppenmetall-Salzen mit Kationen der (maximalen Oxidationsstufe-2) (z.B. Sn2+, Pb2+) kommt es zu einer Verzerrung der Metall-Sauerstoff-Koordination durch das einsame Elektronenpaar. Z.B. sind im Pb2+-Oxid die 6 s2-Elektronen 'stereochemisch aktiv' (sd-Hybrid), so dass PbO und auch SnO eine tetragonal verzerrte CsCl-Struktur ausbilden (Abb. 4.2.3.). Auch die Struktur der gemischtvalenten Verbindung Mennige, Pb3O4, (Abb. 4.2.4.) ist ein schönes Beispiel für die stereochemische Aktivität des 'nichtbindenden Lone-Pairs'.
 |
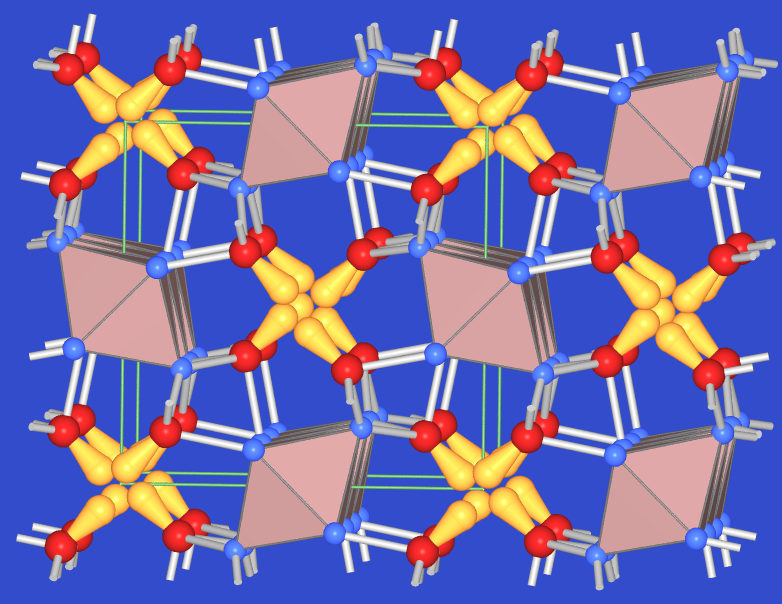 |
| Abb. 4.2.3. Struktur von PbO ‣VRML | Abb. 4.2.4. Struktur von Mennige ‣VRML |
zu 2: Ligandenfeldeinfluß
In die Gitterenergie UL gehen bei Übergangsmetall-Ionen mit
unvollständig gefüllten d-Elektronenschalen neben den elektrostatischen
Anteilen Ec und Er und kovalenten Bindungsanteilen, van der Waals Anteilen usw. auch
die sog. Ligandenfeldstabilisierungsenergien (LFSE, Es) ein. Die Gitterenergie ist damit in
diesen Fällen entsprechend größer.
Der Einfluß der d-Elektronen auf das Koordinationspolyeder um
Übergangsmetall-Kationen ist aus der Komplexchemie (mit Video dazu!) bekannt
(s. auch Erinnerung unten).
Aus der Ligandenfeld-Theorie folgt, dass die Ligandenfeldstabilisierungsenergie (LFSE)
bestimmt, welches Ion welche Koordination (hier gegen den 'Liganden' O2-) bevorzugt.
|
Erinnerung: Liganden- (LF) oder Kristallfeld-Theorie Während sich in den isolierten Kationen alle d-Orbitale auf dem gleichen energetischen Niveau befinden, wird bei der LF-Theorie der Einfluß der Liganden auf die Energieniveaus der verschiedenen d-Orbitale betrachtet. Beispielsweise geben sich im oktaedrischen und im tetraedrischen Ligandenfeld Aufspaltungen der d-Orbitale in zwei Gruppen:
Generell gilt, dass die Aufspaltung im oktaedrischen Ligandenfeld
etwa doppelt so groß ist wie die im tetraedrischen Fall.
Die sog. Spektrochemischen Reihen reihen die Liganden und die Metall-Ionen/Atome nach der Grösse der Aufspaltung. Für die Liganden:
... und für die Metalle/Metallionen:
Fazit: Bei einfachen Salzen wie Oxiden oder Halogeniden ist die Aufspaltung generell eher klein. Die spektrochemische Reihe der Liganden (I- < S2- < F- = O2- < ... < OH-, s.o. ) zeigt, dass O2- ein eher schwacher Ligand ist, so dass Oxide und Halogenide der 3d-Metalle im allgemeinen High-Spin-Kationen enthalten. Erst die 4d- und vor allem die 5d-Metall-Ionen liegen dann im LS-Zustand vor.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Die Kristallfeldstabilisierungsenergie (die in die Gitterenergie direkt mit eingeht) ist die Energie, die durch Einfüllen der Elektronen in die jeweils niedrigeren Niveaus gewonnen wird. Die Besetzung der Zustände folgt i. A. dem Pauli-Prinzip, die Spin-Paarungsenergie bestimmt, ob High-Spin oder Low-Spin-Systeme gebildet werden. Da die Aufspaltung im oktaedrischen Feld etwa doppelt so groß ist, wie die im tetraedrischen Feld, wird bei Kationen mit d3, d4, d6, d7 und d8-Elektronenkonfiguration i.A. die oktaedrische Umgebung bevorzugt (sog. Octahedral Site Preference Energy). Die folgende Tabelle 4.2.2. gibt einen Überblick über das Ausmaß der Bevorzugung:
| Elektronenkonfiguration | Oktaeder- | Tetraeder- | ||
| Ion | Stabilisierung | Stabilisierung | Differenz | |
| d3 | Cr3+ | 225 | 67 | 158 |
| d5 | Fe3+ | 0 | 0 | 0 |
| d6 | Fe2+ | 50 | 33 | 17 |
| d8 | Ni2+ | 122 | 36 | 86 |
| d10 | Zn2+ | 0 | 0 | 0 |
Dieser Einfluß der d-Elektronenverteilung macht sich z.B. bei den verschiedenen Übergangsmetall-Oxiden unmittelbar bemerkbar:
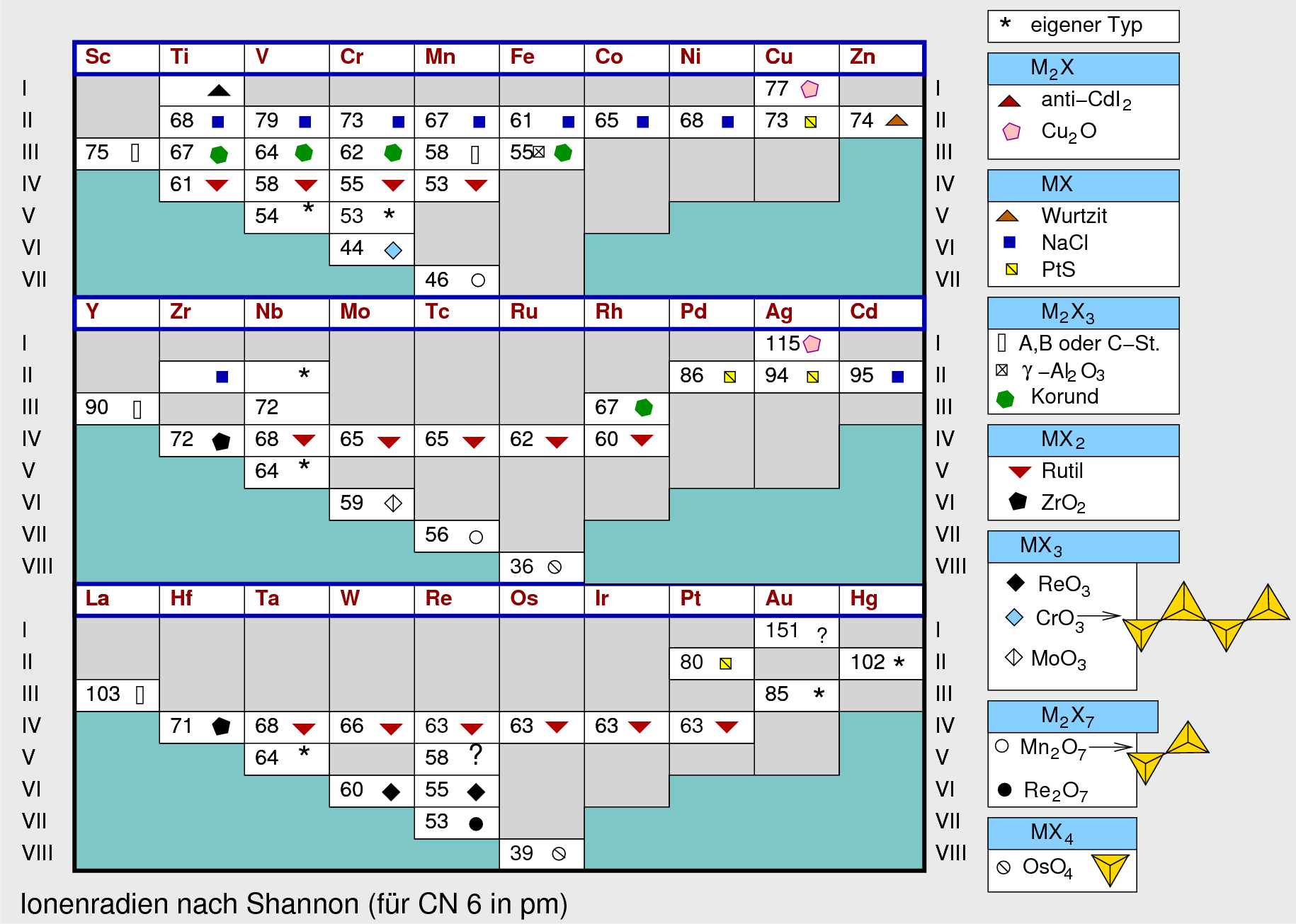 |
| Abb. 4.2.7. Strukturen der Übergangsmetalloxide ‣ SVG |
 |
| Abb. 4.2.8. Struktur von PtS, PtO und PdO ‣VRML |
zu 3: Metall-Metall-Bindungen
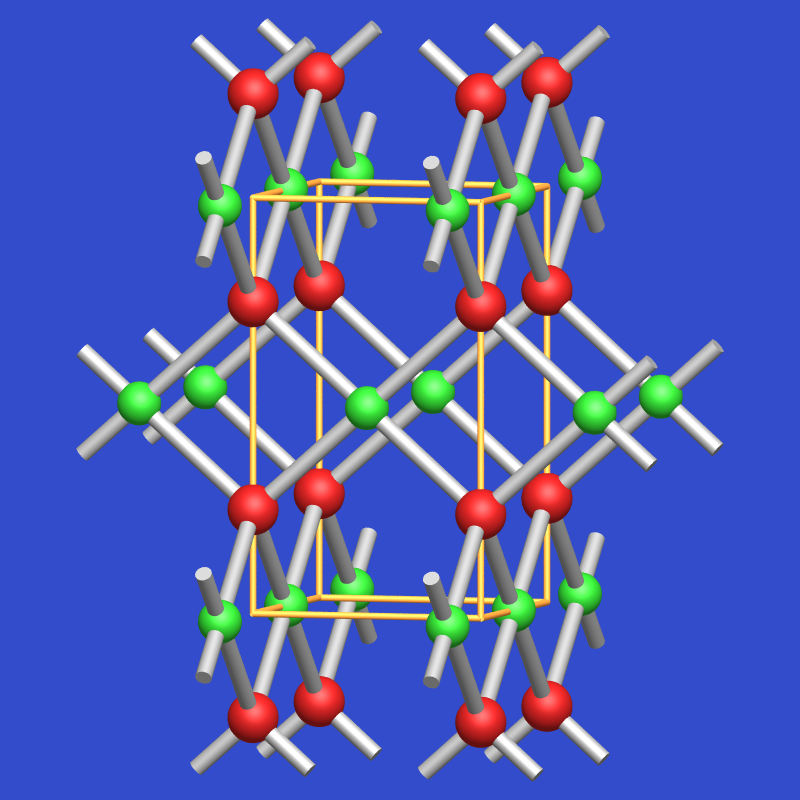
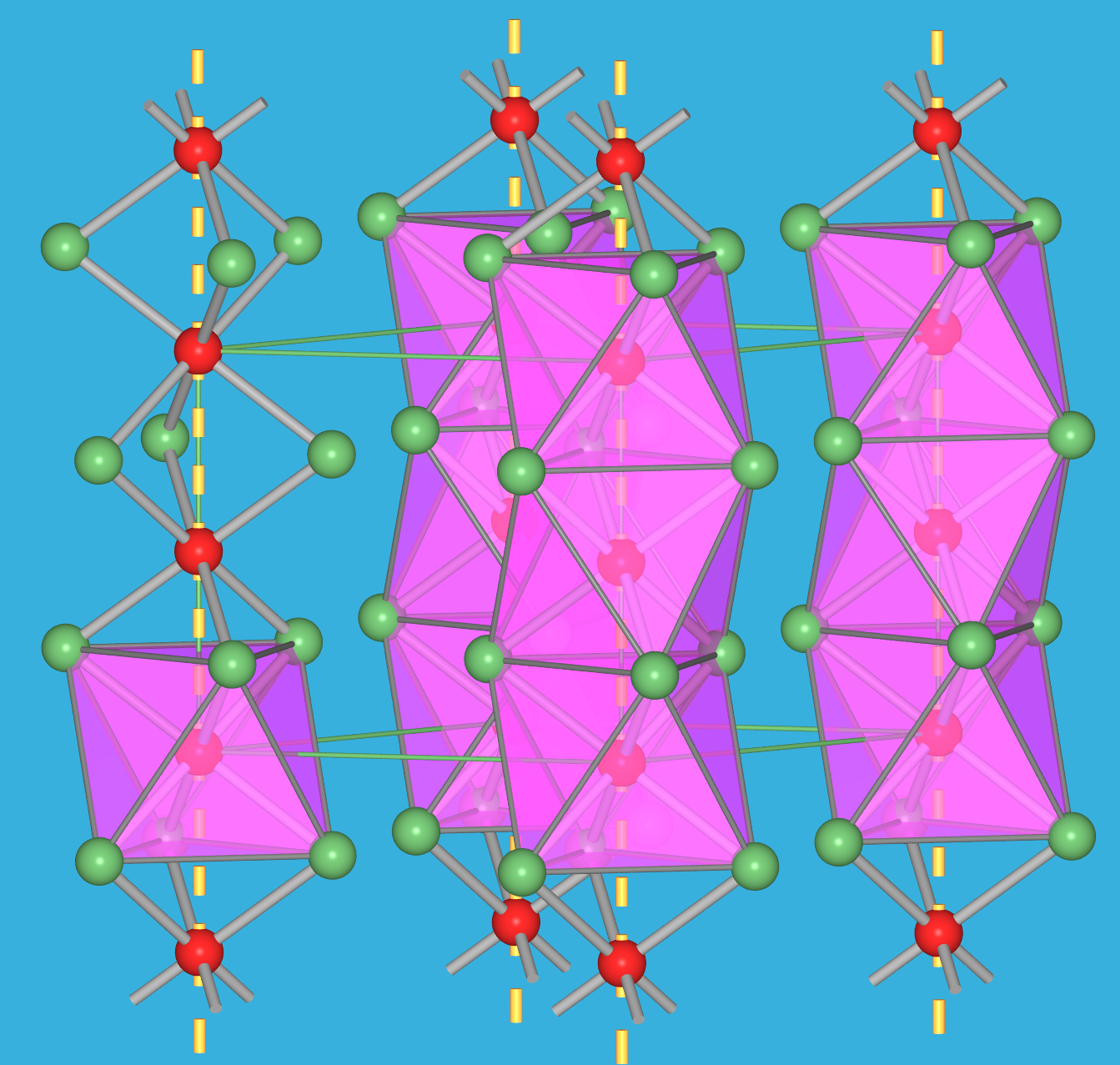
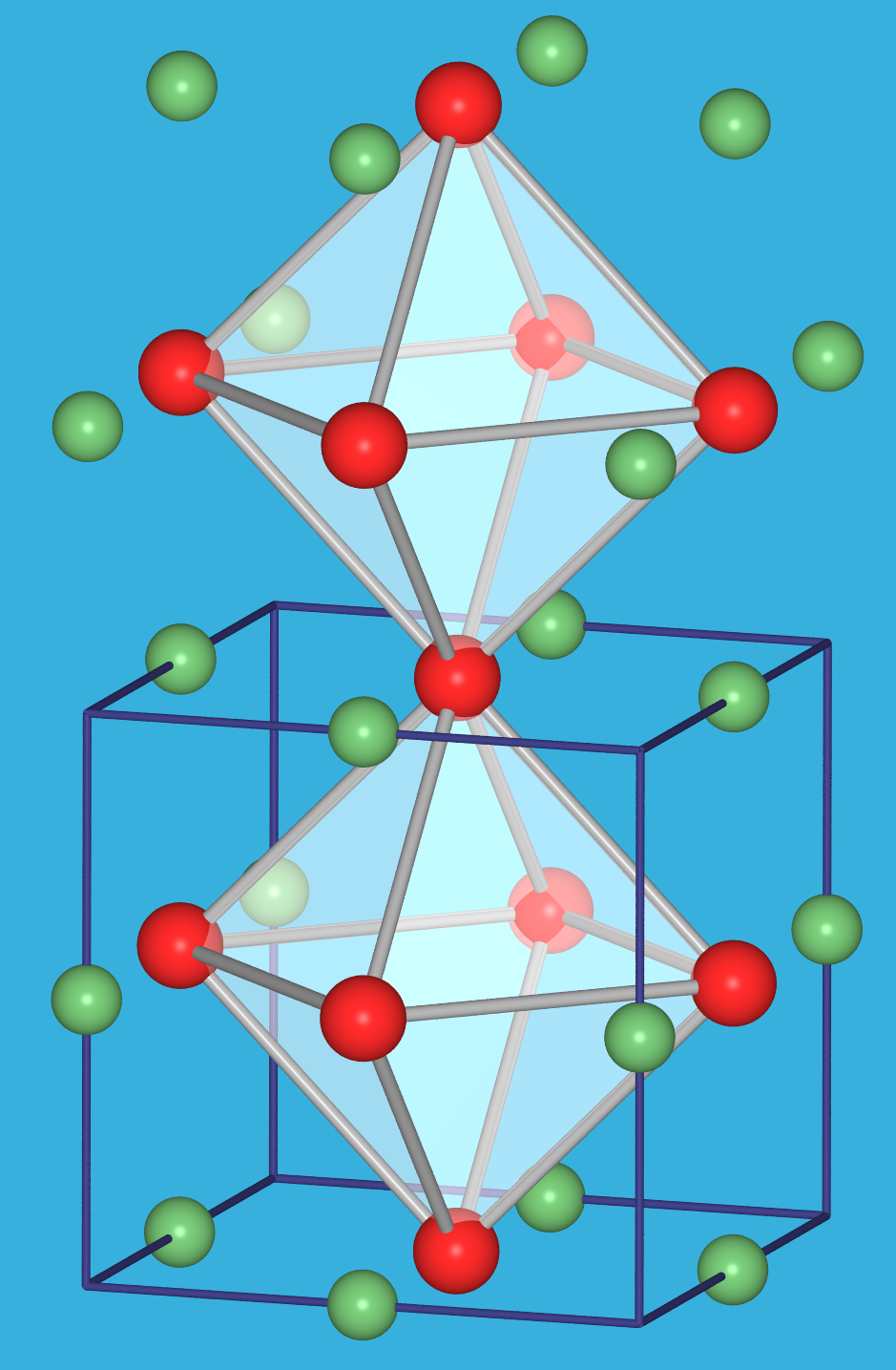
Sobald in Ionenkristallen Metall-Metall-Bindungen auftreten, kommt es zu ungewöhnlichen Strukturen. Das beginnt zunächst mit einer ungewöhnlichen Flächenverknüpfung der Polyeder (z.B. in den Trihalogeniden mit ZrI3-Struktur, s. Abb. 4.2.9) und geht bis hin zur Bildung von Clustern. Typische Beispiele sind hier NbO (Abb. 4.2.10), Wolfram-Halogenide (wie z.B. WCl3 = W6Cl18) oder Chevrell-Phasen. Diese Effekte treten vor allem bei den frühen 4d- und 5d-Übergangsmetall-Ionen auf, die weit ausgedehnte d-Orbitale zeigen (Zr3+, W3+, Nb2+ usw.).
Weitere Beispiele und Informationen zu dieser Art von Clusterverbindungen gibt es HIER.
 |
 |
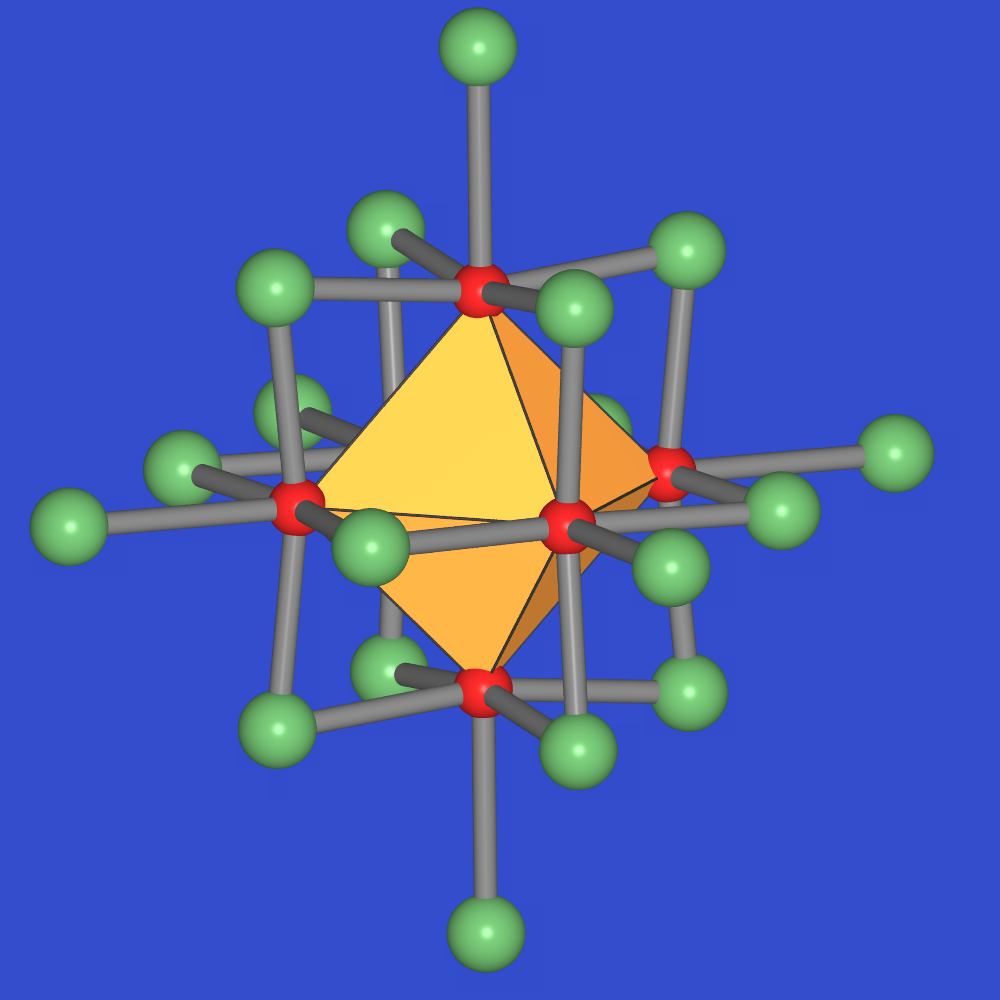 |
| Abb. 4.2.9. Struktur von ZrI3 ‣VRML | Abb. 4.2.10. Struktur von NbO ‣VRML | Abb. 4.2.11. Struktur von WCl3 = W6Cl18 ‣VRML |
| Die Valenz eines Anions in einer stabilen ionischen Struktur versucht die Stärke der elektrostatischen Bindungen der umgebenden Kationen zu kompensieren (und umgekehrt). |
Für jedes Kation i mit der Ladung Q und der Koordinationszahl CNK wird die 'elektrostatische Bindungsstärke' Si angegeben:
Ein stabiles Ionengitter liegt dann vor, wenn die Ladung -X der Anionen der Summe der Bindungsstärken der dieses Anion koordinierenden Kationen entspricht, also gilt:
wobei die Summation über die i Kationen um das jeweilige Anion erfolgt.
Beispiele:
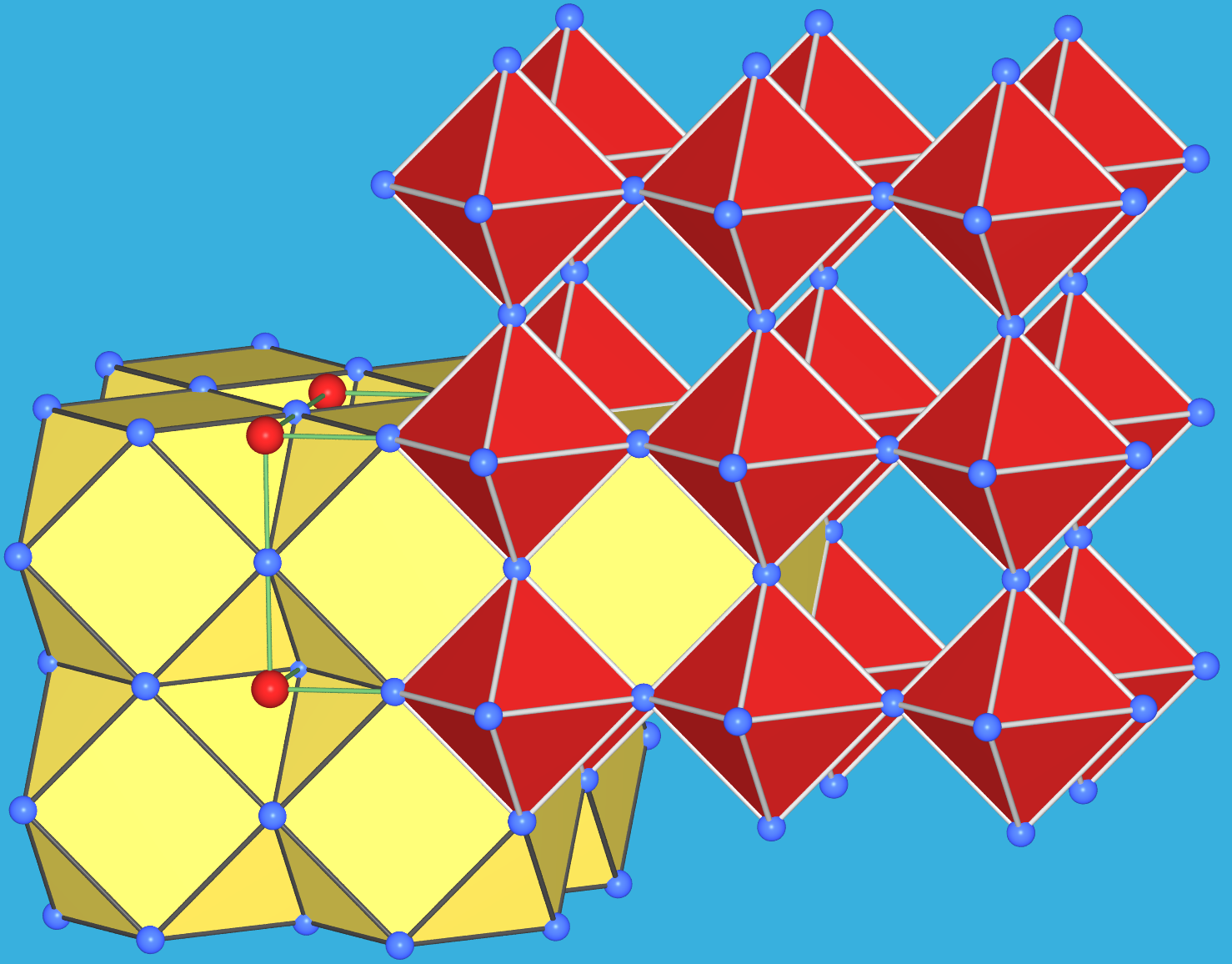 |
| Abb. 4.2.12. Struktur von Perowskit ‣VRML |
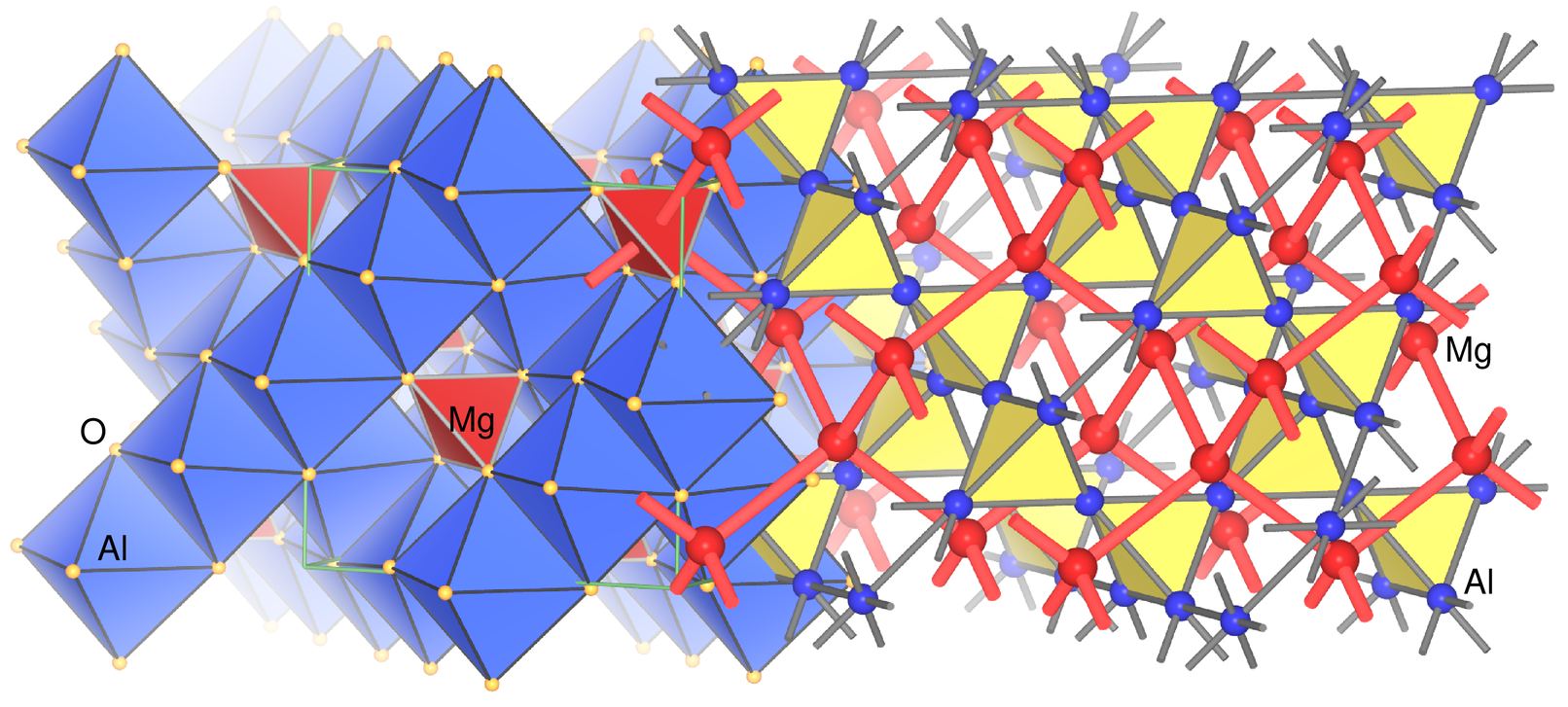 |
| Abb. 4.2.13. Struktur von Spinell. Die Abbildung zeigt links die übliche Polyederdarstellung des gemischten Oxids mit den KKPs, nach rechts sind die Oxid-Ionen weggelassen und man sieht die Analogie zur Laves-Phase MgCu2 und damit auch zur Diamantstruktur (nur Mg) bzw. Cristobalith-Struktur (Al4-Polyeder = SiO4/2-Tetraeder). Bei magnetischen Spinellen haben diese beiden Teilgitter antiparallele Spinorientierung durch antiferromagnetische Kopplung via Superaustausch. ‣VRML |
Zu den Spinellen gibt es im Kapitel 4.4. der Vorlesung Chemie der Metalle noch ein Erklär-Video. Ausserdem kommen die Spinelle AB2O4 im Kapitel 5 der Vorlesung Strukturchemie der Oxide ausführlich vor.
| Teilung von Kanten und besonders von Flächen zwischen Koordinationspolyedern reduziert die Stabilität einer Struktur. Dieser Effekt ist besonders ausgeprägt für Kationen hoher Valenz und geringer Koordinationszahl. |
Bei Salzen mit mehreren Kationen werden diejenigen mit hoher Ladung möglichst weit voneinander weg eingebaut, so dass eine möglichst gute Abschirmung der Kationen voneinander möglich wird. D.h., dass die Kationen-Koordinationspolyeder möglichst wenige Polyederelemente gemeinsam haben sollten.
Beispiele
| In einer Struktur mit mehreren Kationen weichen Kationen mit hohen Ladungen einem Teilen von Bauelementen aus. |
Die Konsequenz z.B. für Alumosilicate ist die sogenannte Löwenstein-Regel, nach der niemals zwei Aluminium-Atome nebeneinander in den Tetraederverband eingebaut sind.
| Die Zahl verschiedener Bauelemente in einer Kristallstruktur ist klein. |
| ⇦ | Inhalt | Einleitung | Kovalente FK | Metalle | Ionenkristalle | Literatur | ⇨ |
| cr_home | Metalle | Nichtmetalle | FK-Chemie | Methoden | Interm. Phasen | Oxide | Silicate | Strukturtypen |