|
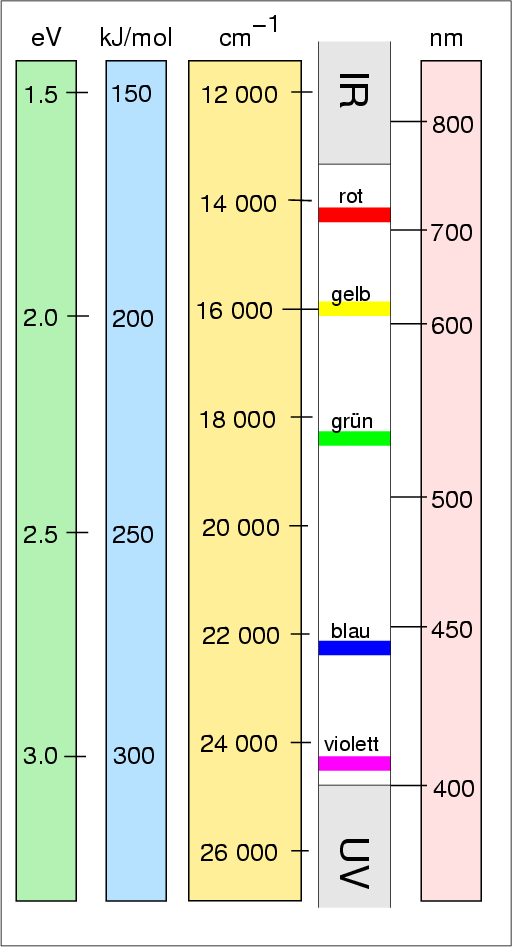
| Abb. I.2.1. Energiebereich der sichtbaren Spektroskopie ‣ SVG |
| cr_home | Metalle | Nichtmetalle | FK-Chemie | Strukturchemie | Interm. Phasen | Oxide | Silicate | Strukturtypen | AFP |
| ← | Inhalt | Einleitung | I. Spektroskopie | II. Beugung | III. Bildgebung | IV. Sonstige Methoden | → |
Vorlagen

|
| Abb. I.2.1. Energiebereich der sichtbaren Spektroskopie ‣ SVG |
| λ | ν | Energie | Farbe | Komplementär- | |
|---|---|---|---|---|---|
| [nm] | [cm-1] | [kJ/mol] | [eV] | . | -farbe |
| 780 | 12 821 | 153.4 | 1.59 | IR-Bereich | |
| 680-700 | rot/violett | grün | |||
| 610-680 | rot | blau/grün | |||
| 595-610 | orange | grün/blau | |||
| 546 | 18 315 | 219.2 | 2.27 | ||
| 500-560 | grün | rot/violett | |||
| 490-500 | blau/grün | rot | |||
| 480-490 | grün/blau | orange | |||
| 435-480 | blau | gelb | |||
| 435 | 22936 | 274.5 | 2.84 | ||
| 400-435 | violett | gelb/grün | |||
| 365 | 27 397 | 327.8 | 3.40 | UV-Bereich | |
| 313 | 31 949 | 382.1 | 3.96 | ||
| 253.7 | 39 417 | 471.7 | 4.89 | ||
| 200 | 50 000 | 598.3 | 6.2 | ||
| 109 678 | 13.596 | ||||
 |
 |
 |
 |
 |
| Aussenansicht | Innenansicht | In-Situ Mess-Stab | ||
| Abb. I.2.2. Fotos von UV-Spektrometern in der Anorganik | ||||
|
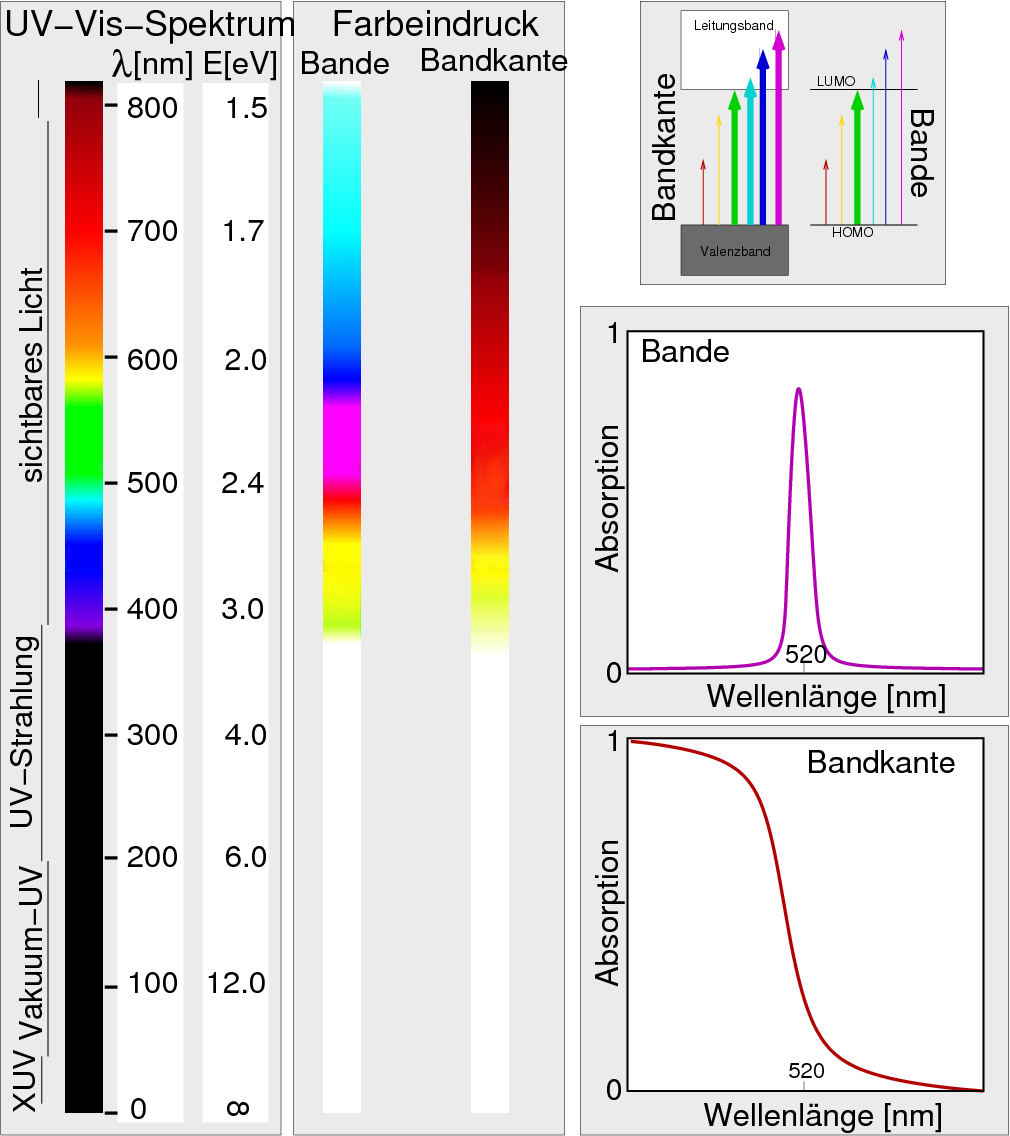
| Abb. I.2.3. Spektrum und Farbeindruck bei (scharfen) Banden- und (breiten) Band-Band-Übergängen ‣ PDF |
| Drehimpuls d mit Quantenzahl d | |||
|---|---|---|---|
| Quantelung | Bahn- | Eigen- | Gesamt- |
| Betrag | |||
| mit | mit | mit | |
| Richtung | |||
| mit | mit | mit | |
| Energien: | |||
| Zahl der Zustände: 2d+1 | |||
|
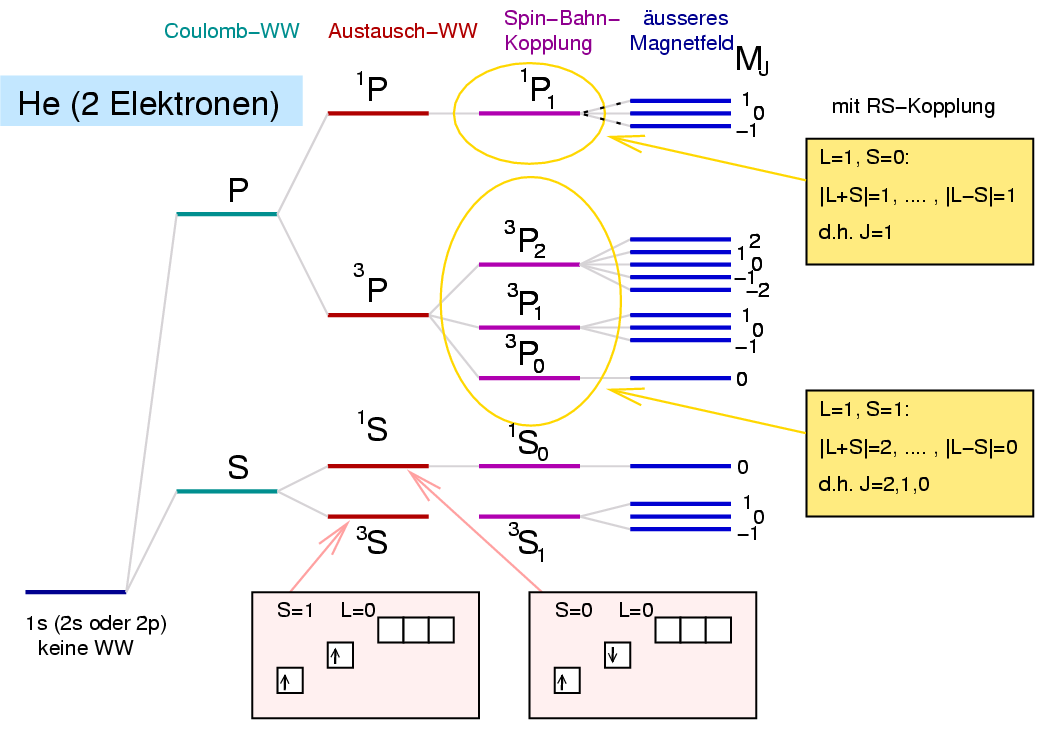
| Abb. I.2.4. Termschema von Helium (Farbkordierung s. auch Tab. I.2.2.) ‣ SVG |
|
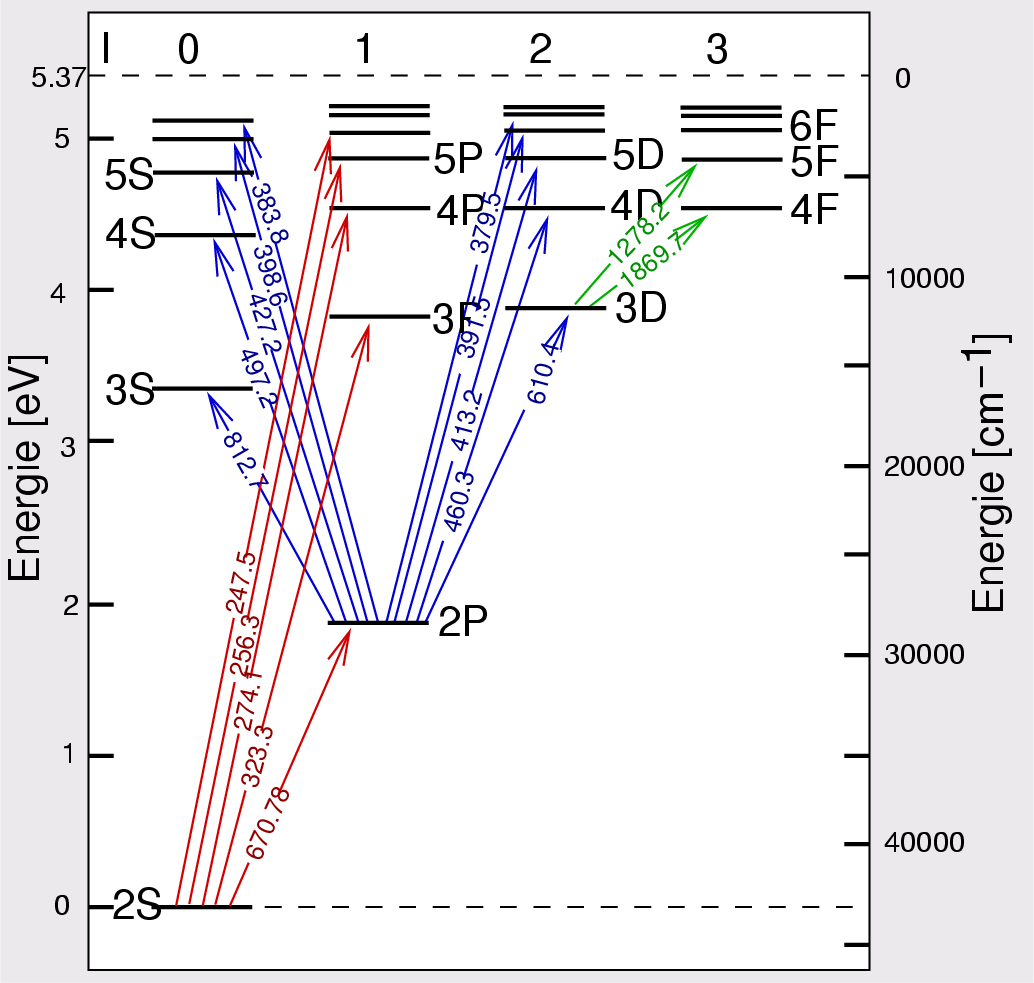
| Abb. I.2.5. Termschema von Lithium, mit erlaubten elektronischen Übergängen ‣ SVG |
|
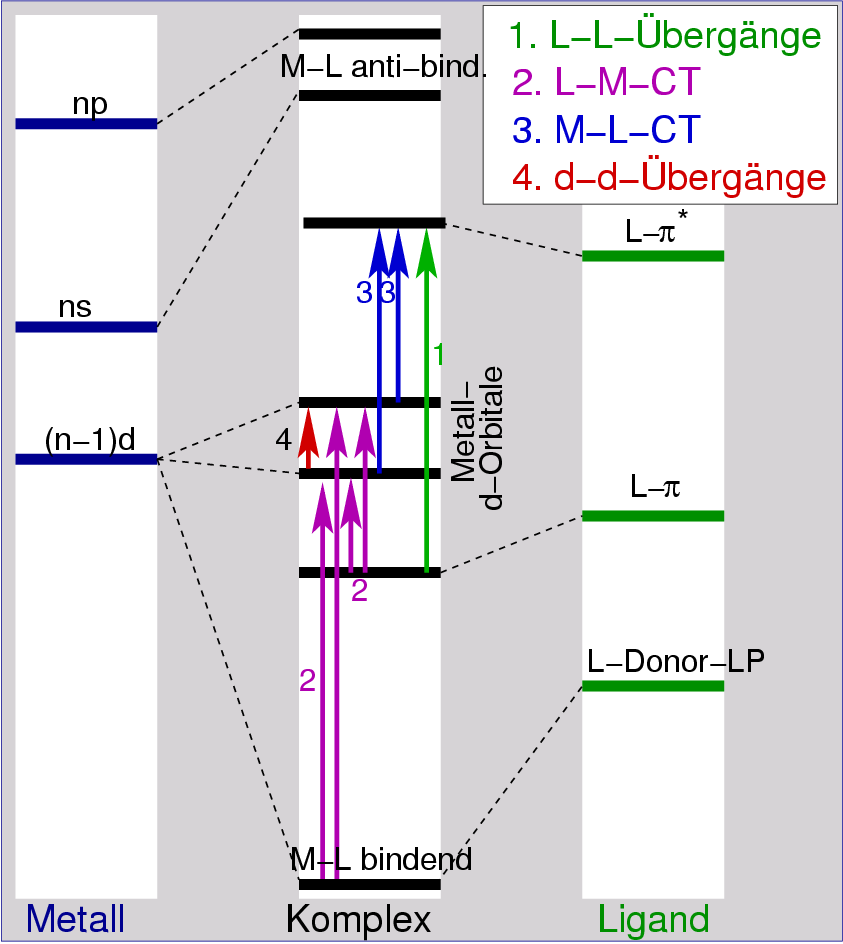
| Abb. I.2.6. Elektronische Übergänge in Komplexen ‣ SVG |
|
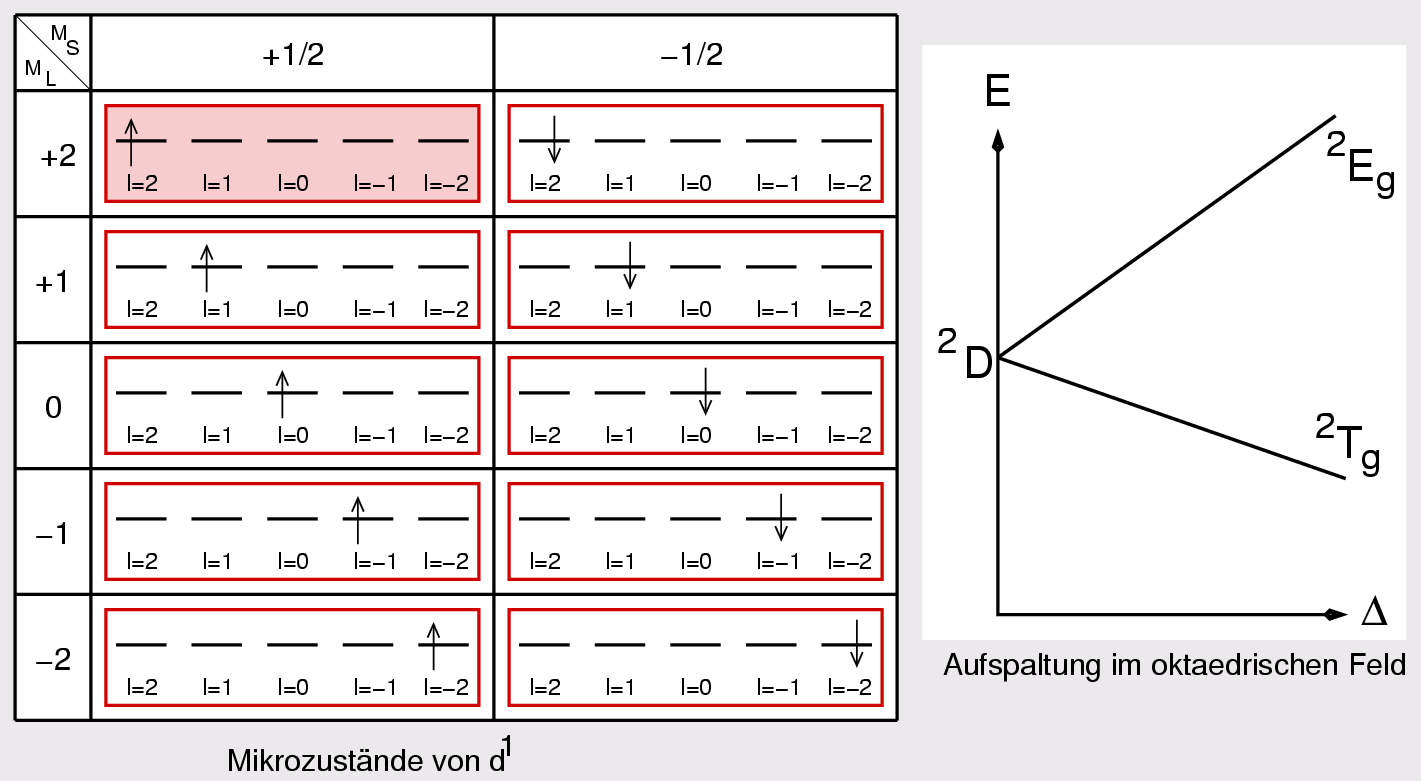
| Abb. I.2.7. Terme für d1-Systeme ‣ SVG |
| RS-Terme | Kristallfeldkomponenten |
|---|---|
| S | A1g |
| P | T1g |
| D | Eg, T2g |
| F | A2g, T1g, T2g |
| G | A1g, Eg, T1g, T2g |
| H | Eg, 2 T1g, T2g |
| I | A1g, A2g, Eg, T1g, 2 T2g |
|
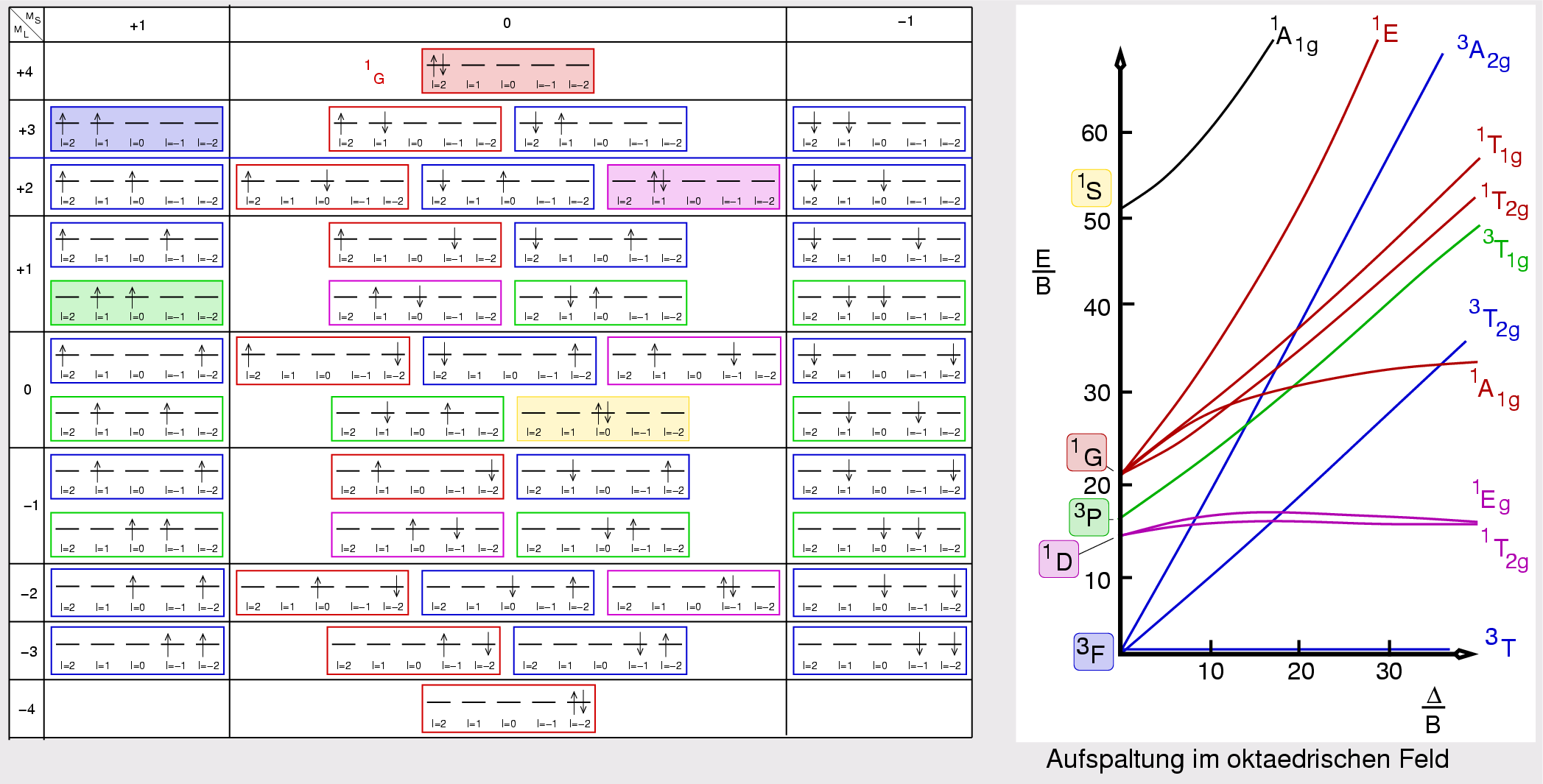
| Abb. I.2.8. Terme für d2-Systeme ‣ SVG |
| Elektronen-Konfiguration | Terme |
|---|---|
| d1, d9 | 2D |
| d2, d8 | 3F, 3P, 1G, 1D, 1S |
| d3, d7 | 4F, 4P, 2H, 2G, 2F, 2 2D, 2P |
| d4, d6 | 5D, 3H, 3G, 2 3F, 3D, 2 3P, 1I, 2 1G, 1F, 2 1D, 2 1S |
| d5 | 6S, 4G, 4F, 4D, 4P, 2I, 2H, 2 2G, 2 2F, 3 2D, 2I, 2S |
|
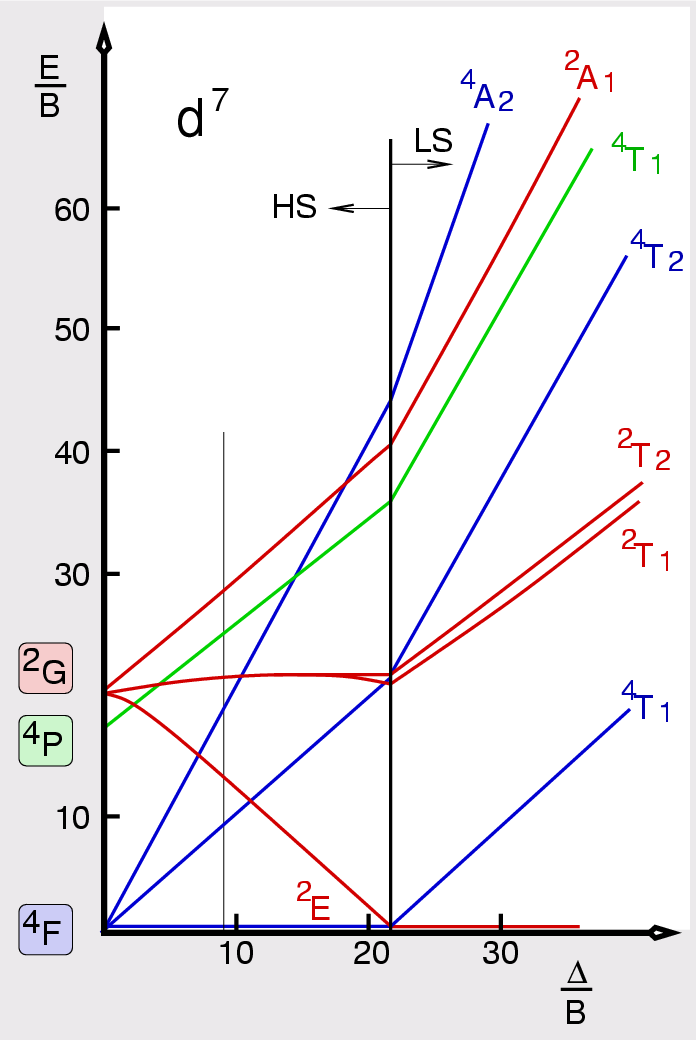
| Abb. I.2.9. Terme für d7-Systeme ‣ SVG |
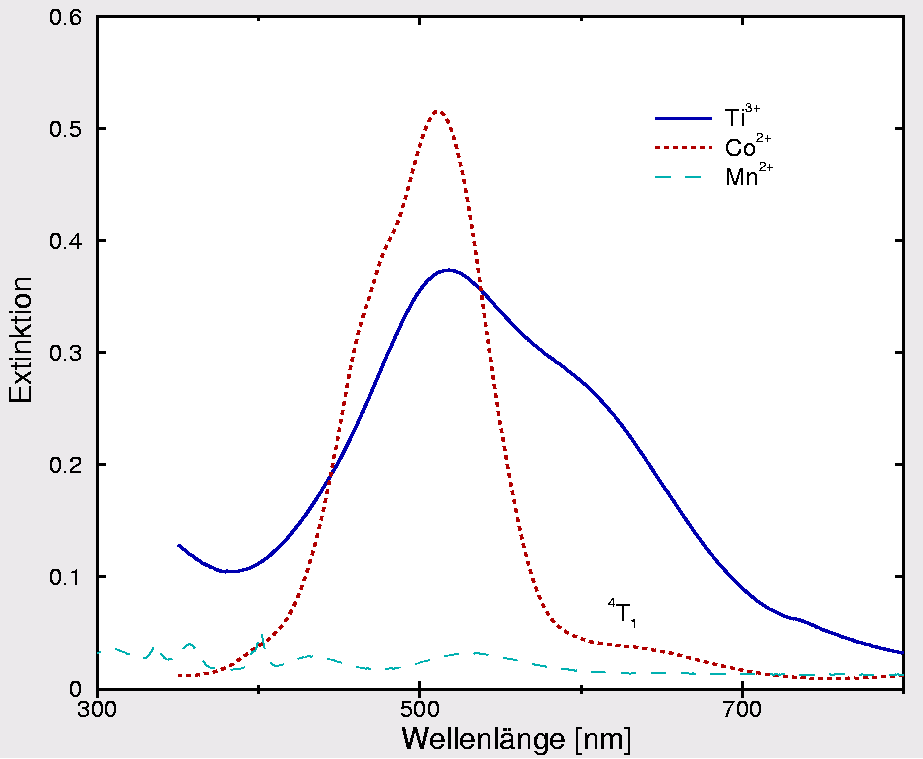
|
| Abb. I.2.10. UV-Spektren verschiedener Hexaquakomplexe ‣ SVG |
 |
 |
 |
| Gelb 6 GS (Zn,Cd)S | Orange 3 RS Cd(S,Se) | Rot BS Cd(S,Se) |
| Abb. I.2.11. Verschiedene Sulfid/Selenid-Pigmente | ||
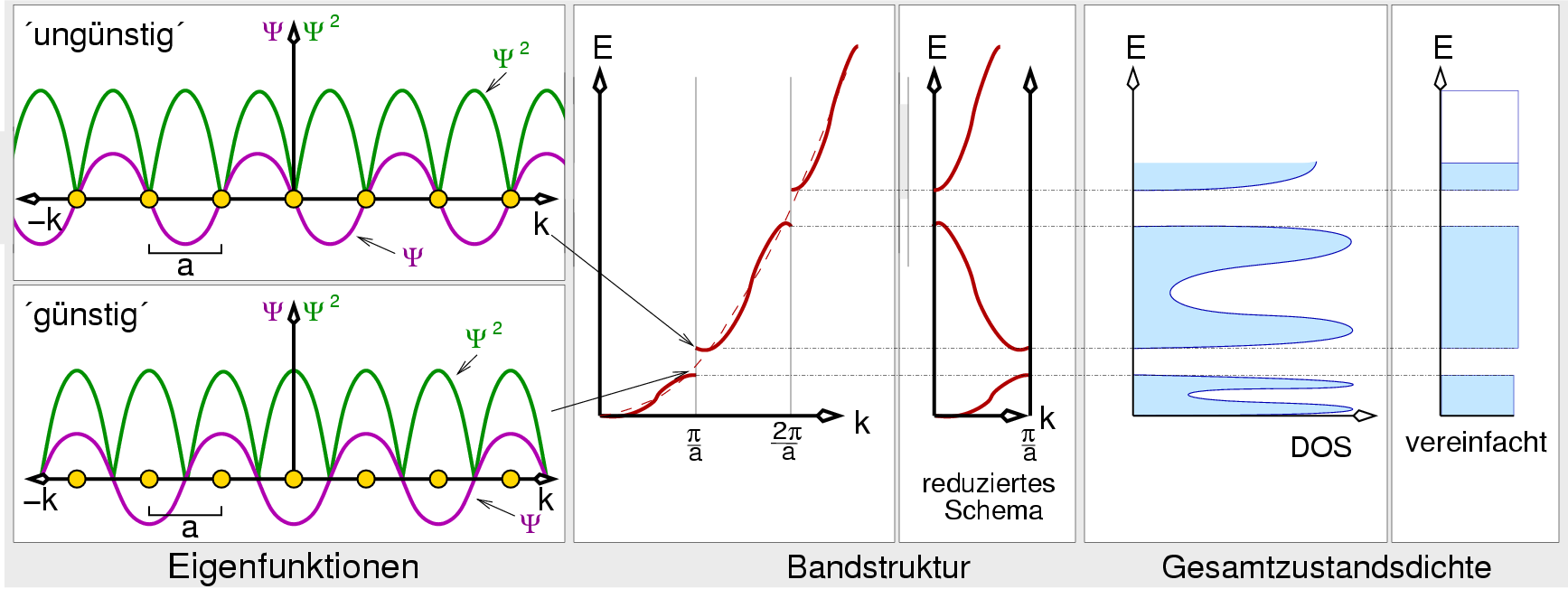
|
| Abb. I.2.12. Lösungen von Teilchen im Kasten (mit Kernpotentialen) ‣ SVG |
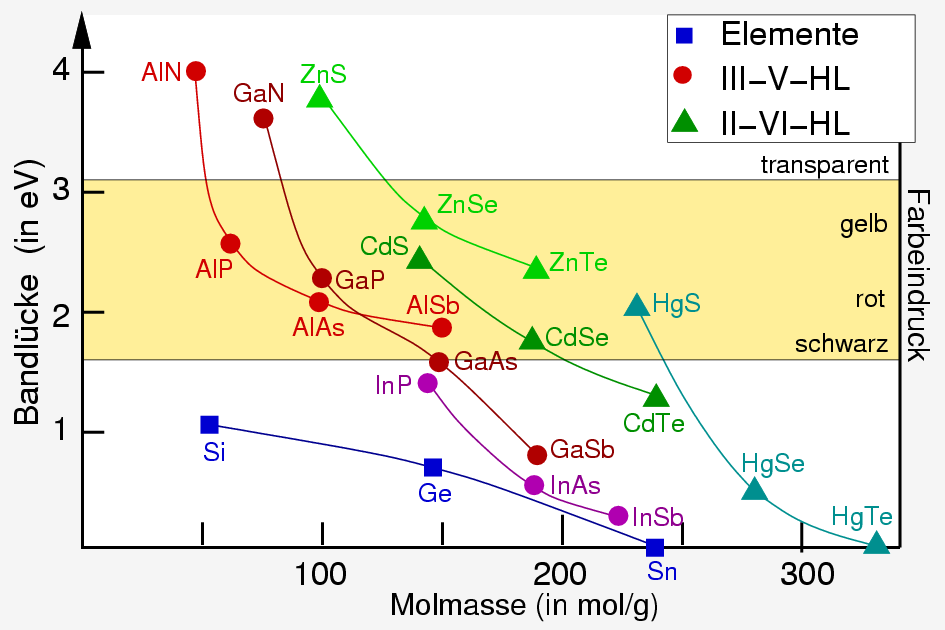
|
| Abb. I.2.13. Energiebereich der sichtbaren Spektroskopie ‣ SVG |
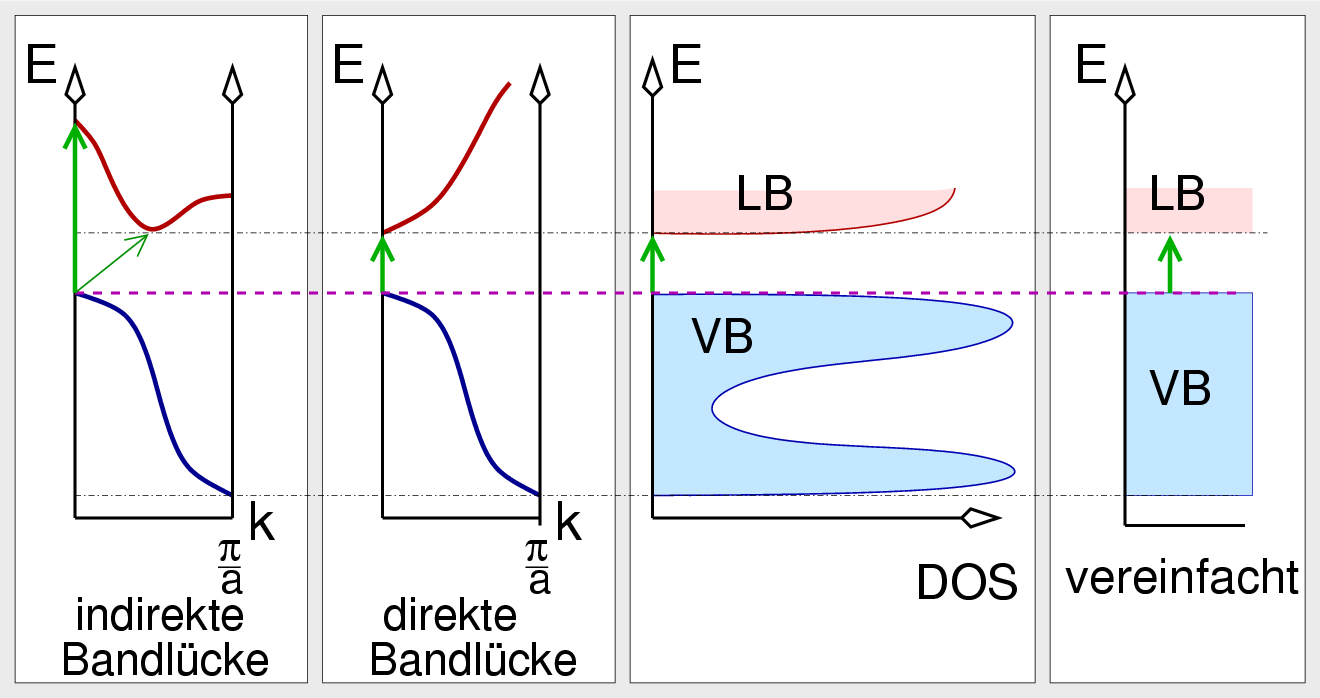
|
| Abb. I.2.14. Energiebereich der sichtbaren Spektroskopie ‣ SVG |
| ← | Inhalt | Einleitung | I. Spektroskopie | II. Beugung | III. Bildgebung | IV. Sonstige Methoden | → |
| cr_home | Metalle | Nichtmetalle | FK-Chemie | Strukturchemie | Interm. Phasen | Oxide | Silicate | Strukturtypen | AFP |